Sprinter
Úloha číslo: 108
Sprinter měl při tréninku na trati délky 100 m vymezený úsek, na kterém se měl rozbíhat rovnoměrně zrychleným pohybem a dosaženou rychlostí pak pokračovat do cíle. Trenér nejprve stanovil délku zrychleného úseku na 36 m a naměřil na něm čas 9 s, podruhé stanovil délku tohoto úseku na 30 m a naměřil na něm čas 7 s.
a) Určete dosaženou maximální rychlost při prvním a druhém rozběhu a konečné časy na celé dráze 100 m při prvním a druhém rozběhu.
b) Určete maximální rychlost, které by při třetím rozběhu musel sprinter dosáhnout na stejném úseku jako při druhém rozběhu a kterou by poté udržel do cíle, aby doběhl v konečném čase 12 s.
c) Sestrojte do jednoho obrázku grafy závislosti rychlosti na čase všech tří běhů.
d) Určete zrychlení sprintera při rozbíhání v každém z uvedených běhů.
Poznámka: Přesněji bychom měli mluvit o velikosti rychlosti a velikosti zrychlení. Vzhledem k tomu, že jde o přímočarý pohyb, kde se směr těchto veličin nemění, píšeme pro přehlednost a zkrácení textu jen rychlost a zrychlení.
Zápis
s = 100 m celková dráha s1 = 36 m délka zrychleného úseku při 1. rozběhu t1 = 9 s čas na zrychleném úseku při 1. rozběhu s2 = 30 m délka zrychleného úseku při 2. rozběhu t2 = 7 s čas na zrychleném úseku při 2. rozběhu a) vm1 = ? (m·s−1) maximální rychlost při 1. rozběhu vm2 = ? (m·s−1) maximální rychlost při 2. rozběhu tk1 = ? (s) celkový čas při 1. rozběhu tk2 = ? (s) celkový čas při 2. rozběhu b) s3 = s2 = 30 m délka zrychleného úseku při 3. rozběhu tk3 = 12 s celkový čas při 3. rozběhu t3 = ? (s) čas na na zrychleném úseku při 3. rozběhu vm3 = ? (m·s−1) maximální rychlost při 3. rozběhu d) a1 = ? (m·s−2) zrychlení na zrychleném úseku při 1. rozběhu a2 = ? (m·s−2) zrychlení na zrychleném úseku při 2. rozběhu a3 = ? (m·s−2) zrychlení na zrychleném úseku při 3. rozběhu Nápověda 1 pro a): Maximální rychlosti
Uvědomte si, jaké vztahy platí pro rychlost a dráhu rovnoměrně zrychleného pohybu. Spojením těchto vztahů snadno určíte dosaženou maximální rychlost vm1 a vm2.
Nápověda 2 pro a): Konečné časy na dráze
Pro určení konečného času si stačí uvědomit, že čas na zrychleném úseku známe a čas sprintera na úseku, kde se pohyboval rovnoměrně, snadno určíme z délky daného úseku a výše určené dosažené maximální rychlosti.
Nápověda 3 pro b): Maximální rychlost pro třetí běh
Víte, jaký platí vztah mezi dráhou, dobou a rychlostí rovnoměrného pohybu?
Dráhu, na které se sprinter pohyboval rovnoměrně, snadno odvodíte, stejně tak dobu, kterou tento úsek běžel. Rychlost hledáme. Pro neznámý čas běhu sprintera na zrychleném úseku pak stačí buď použít vztah z předchozí úlohy, nebo si uvědomit, jak se dá vyjádřit doba rovnoměrně zrychleného pohybu.
Nápověda 4 pro c): Grafy závislosti rychlosti na čase
K sestrojení grafů musíte dopočítat čas t3 . Vztah pro jeho výpočet znáte z předchozí části úlohy.
Které veličiny ještě k sestrojení grafů potřebujete? Znáte je všechny?
Nápověda 5 pro d): Zrychlení sprintera při rozbíhání
Stačí vyjít ze vztahu mezi zrychlením a rychlostí rovnoměrně zrychleného pohybu.
Všechny veličiny pak již znáte.
CELKOVÉ ŘEŠENÍ
a) Z rovnic
\[v_\mathrm{m1}\,=\,a_1t_1\,,\] \[s_1\,=\,\frac{1}{2}a_1t_1^{2}\,\]plyne:
\[v_\mathrm{m1}\,=\,\frac{2s_1}{t_1}\,.\]Číselně:
\[v_\mathrm{m1}\,=\,\frac{2{\cdot}36}{9}\,\mathrm{m\cdot s^{-1}} \,=\,8\,\mathrm{m\cdot s^{-1}}\,.\]Čas dosažený na celé dráze při prvním běhu je:
\[t_\mathrm{k1}=t_1+ t_1^{,}\,,\]kde
\[ t_1^{,} \,=\, \frac{s-s_1}{v_\mathrm{m1}}\,.\]Dosadíme za vm1:
\[ t_1^{,} \,=\, \frac{(s-s_1)t_1}{2s_1}\,.\]Pak:
\[t_\mathrm{k1}\,=\,t_1 + \frac{(s-s_1)t_1}{2s_1} \,=\, \frac{2s_1t_1 + st_1 - s_1t_1}{2s_1} \,=\, \frac{s+s_1}{2s_1}\,t_1\,.\]Číselně:
\[t_\mathrm{k1}\,=\,\frac{100 + 36}{2{\cdot}36}\cdot9\,\mathrm{s}\,\dot=\,17\,\mathrm{s}\,.\]Analogicky pro druhý běh:
\[v_\mathrm{m2}\,=\,\frac{2s_2}{t_2}\,.\]Číselně:
\[v_\mathrm{m2}\,=\,\frac{2{\cdot}30}{7}\,\mathrm{m\cdot s^{-1}}\,\dot=\,8{,}6\,\mathrm{m\cdot s^{-1}}\,.\]Pro čas dosažený na celé dráze při druhém běhu platí:
\[t_\mathrm{k2}\,=\,\frac{s+s_2}{2s_2}t_2\,.\]Číselně:
\[t_\mathrm{k2}\,=\,\frac{100 + 30}{2{\cdot}30}\cdot7\,\mathrm{s}\,\dot=\,15{,}2\,\mathrm{s}\,.\]b) Při třetím běhu platí:
\[s\,-\,s_3\,=\,v_\mathrm{m3}(t_\mathrm{k3}-t_3)\,=\,v_\mathrm{m3}\left(t_\mathrm{k3}-\frac{2s_3}{v_\mathrm{m3}}\right)\,=\,v_\mathrm{m3}t_\mathrm{k3}\,-\,2s_3\,,\] \[v_\mathrm{m3}\,=\,\frac{s+s_3}{t_\mathrm{k3}}\,.\]Číselně:
\[v_\mathrm{m3}\,=\,\frac{100+30}{12}\,\mathrm{m\cdot s^{-1}}\,=\,10{,}8\,\mathrm{m \cdot s^{-1}}\,.\]c) K sestrojení grafů je nutné dopočítat čas t3 :
\[t_3\,=\,\frac{2s_3}{v_\mathrm{m3}}\,=\,\frac{2s_3}{s+s_3}t_\mathrm{k3}\,.\]Číselně:
\[t_3\,=\,\frac{2{\cdot}30}{100+30}\cdot12\,\mathrm{s}\,=\,5{,}5\,\mathrm{s}\,.\]Zbývající veličiny t1, t2, tk1, tk2, tk3, vm1, vm2 a vm3 už známe.
d) Zrychlení při rozbíhání při jednotlivých pohybech jsou následující:
\[a_1\,=\,\frac{v_\mathrm{m1}}{t_1}\,=\,\frac{2s_1}{{t_1}^{2}}\,,\] \[a_2\,=\,\frac{v_\mathrm{m2}}{t_2}\,=\,\frac{2s_2}{{t_2}^{2}}\,,\] \[a_3\,=\,\frac{v_\mathrm{m3}}{t_3}\,=\,\frac{2s_3}{{t_3}^{2}}\,=\,\frac{(s+s_3)^{2}}{2s_3{t_\mathrm{k3}}^{2}}\,.\]Číselně:
\[a_1\,=\,\frac{2{\cdot}36}{{9}^{2}}\,\mathrm{m\cdot s^{-2}}\,\dot=\,0{,}9\,\mathrm{m\cdot s^{-2}}\,,\] \[a_2\,=\,\frac{2{\cdot}30}{{7}^{2}}\,\mathrm{m\cdot s^{-2}}\,\dot=\,1{,}2\,\mathrm{m\cdot s^{-2}}\,,\] \[a_3=\frac{(100+30)^{2}}{2{\cdot}30\cdot12^{2}}\,\mathrm{m\cdot s^{-2}}\,\dot=2{,}0\,\mathrm{m\cdot s^{-2}}\,.\]Odpověď
a) Dosažené maximální rychlosti jsou
\[v_\mathrm{m1}\,=\,\frac{2s_1}{t_1}\,=\,8\,\mathrm{m\cdot s^{-1}}\,,\] \[v_\mathrm{m2}\,=\,\frac{2s_2}{t_2}\,\dot=\,8{,}6\,\mathrm{m\cdot s^{-1}}\,.\]Konečné časy na celé dráze jsou
\[t_\mathrm{k1}\,=\,\frac{s+s_1}{2s_1}t_1\,\dot=\,17\,\mathrm{s}\,,\] \[t_\mathrm{k2}\,=\,\frac{s+s_2}{2s_2}t_2\,\dot=\,15{,}2\,\mathrm{s}\,.\]b) Maximální dosažená rychlost při třetím běhu je
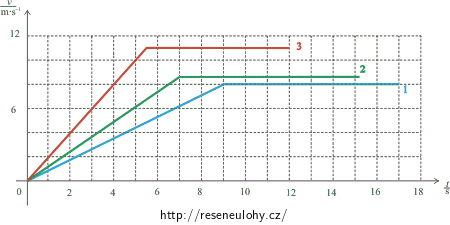
\[v_\mathrm{m3}\,=\,\frac{s+s_3}{t_\mathrm{k3}}\,\dot=\,10{,}8\,\mathrm{m\cdot s^{-1}}\,.\]c) Grafy závislosti rychlosti na čase u všech tří běhů:
d) Zrychlení sprintera při rozbíhání v každém z uvedených běhů jsou
\[a_1\,=\,\frac{v_\mathrm{m1}}{t_1}\,\dot=\,0{,}9\,\mathrm{m\cdot s^{-2}}\,,\] \[a_2\,=\,\frac{v_\mathrm{m2}}{t_2}\,\dot=\,1{,}2\,\mathrm{m\cdot s^{-2}}\,,\] \[a_3\,=\,\frac{v_\mathrm{m3}}{t_3}\,\dot=\,2{,}0\,\mathrm{m\cdot s^{-2}}\,.\]