Sbírka řešených úloh

Pole kondenzátoru s dvěma dielektriky

Úloha číslo: 241

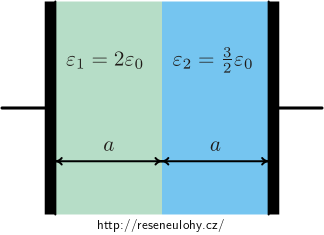
Prostor mezi deskami deskového kondenzátoru je vyplněn dvěma bloky lineárního dielektrika; každý z nich má šířku a, takže celková vzdálenost elektrod je 2a. Jedno dielektrikum má relativní permitivitu 2, druhé 1,5. Nábojová hustota volného náboje na deskách kondenzátoru je ± σ. Určete

(a) elektrickou indukci pole \(\vec D\) v obou blocích,

(b) elektrickou intenzitu pole \(\vec E\) v obou blocích,

(c) polarizaci \(\vec P\) v obou blocích,

(d) potenciálový rozdíl mezi elektrodami,

(e) rozložení a velikost vázaného náboje.

(f) Znovu vypočtěte intenzitu elektrického pole v každém bloku, tentokrát ze znalosti rozložení veškerého (volného i vázaného) náboje. Potvrďte tak správnost výpočtu v bodě (b).

• Nápověda — část (a)

  Pro část (a) použijte Gaussovu větu elektrostatiky pro elektrickou indukci a volné náboje. Použijte ji na kvádr, který je v polovině rozťat kladnou elektrodou a neprotíná elektrodu zápornou. Uvažujte, že desky kondenzátoru jsou veliké (takřka nekonečné roviny), takže z důvodu rovinné symetrie bude vektor indukce na desky kondenzátoru kolmý.

• Nápověda — části (b) až (d)

  Ze spočtené indukce, díky linearitě dielektrika, vypočtěte intenzitu elektrického pole pomocí zadané permitivity. Z intenzity a indukce vypočtěte polarizaci. Znalost intenzity též použijte k výpočtu potenciálového rozdílu mezi deskami (nebo si celou situaci představte jako dva deskové kondenzátory spojené do série).

• Nápověda – část (e)

  Ze znalosti polarizace určete vázané náboje; dejte pozor, povrchy jsou dva a dva pro každé dielektrikum, tedy celkem čtyři!

• Nápověda – část (f)

  Pro výpočet pole pomocí volných a vázaných nábojů můžete znovu použít Gaussovu větu elektrostatiky, tentokrát pro elektrickou intenzitu a celkový náboj.

• Rozbor

  Předpokládejme, že desky kondenzátoru jsou velké (téměř nekonečné roviny). Ze symetrie situace plyne, že elektrická indukce mezi deskami bude mít směr kolmý na desky a bude orientována od kladné k záporné. Pole vně desek je nulové.

  To nám umožní aplikovat Gaussovu větu pro elektrickou indukci na kvádr, který je uprostřed rozťat na dvě poloviny kladně nabitou deskou a neprotíná zápornou desku. Odtud určíme velikost elektrické indukce mezi deskami.

  Ze znalosti elektrické indukce pak můžeme vypočíst elektrickou intenzitu v obou dielektrikách, díky předpokladu, že obě dielektrika jsou lineární. Ze znalosti intenzity a indukce jednoduše vypočteme polarizaci, znalost polarizace ihned dává přímým výpočtem rozložení vázaného náboje.

  Z vypočtené intenzity pole v každém bloku určíme potenciálový rozdíl mezi deskami. Protože všechny body každé elektrody musí mít stejný potenciál, stačí kolmicí spojit dva body obou elektrod a provést integraci intenzity podél této kolmice.

  Nebo můžeme bloky dielektrika považovat za dva kondenzátory spojené do série a použít vztah pro napětí v deskovém kondenzátoru.

  Známe-li nyní rozložení vázaného i volného náboje, můžeme standardními metodami určit intenzitu pole v jednotlivých oblastech. Například, vzhledem k symetrii situace, můžeme opět použít Gaussovu větu, tentokrát ve verzi s elektrickou intenzitou a celkovým nábojem.

• Řešení částí (a) až (d)

  (a) Ze symetrie vyplývá, že elektrická indukce bude mít směr od kladně nabité elektrody k záporně nabité. Vztah

  \[\oint_\mathrm{S} \vec D\cdot\,d\vec S = Q_{\mathrm{vol}}\]

  aplikujeme na kvádr, který je uprostřed protnut kladně nabitou elektrodou a neprotíná druhou elektrodu (viz obrázek). „Pole teče“ pouze mezi elektrodami. Tok je tedy nenulový pouze jedinou stěnou S kvádru rovnoběžnou s elektrodou, proto

  \[D\cdot S = Q = \sigma S \Rightarrow D = \sigma.\]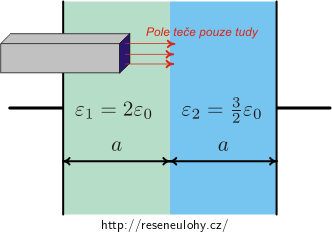

  

  (b) Využijeme vztahů pro lineární dielektrikum. V prvním bloku dostaneme

  \[E_1 = \frac{D}{\varepsilon_1} = \frac{\sigma}{\varepsilon_1} = \frac{\sigma}{2\varepsilon_0},\]

  v druhém bloku

  \[E_2 = \frac{D}{\varepsilon_2} = \frac{\sigma}{\varepsilon_2} = \frac{2\sigma}{3\varepsilon_0}.\]

  Elektrická intenzita má stejný směr a orientaci jako elektrická indukce.

  (c) Polarizace má stejný směr a orientaci jako elektrická intenzita. Pro její velikost máme

  \[P = D-\varepsilon_0 E = \varepsilon E- \varepsilon_0 E = \varepsilon_0(\varepsilon_r-1)E.\]

  Odtud po dosazení

  \[P_1 = \frac{\sigma}{2}, \qquad P_2 = \frac{\sigma}{3}.\]

  (d) Potenciálový rozdíl vypočteme integrací: integrujeme po kolmici k oběma elektrodám, která spojuje její libovolné dva body (například tedy po šipkách naznačujících tloušťku dielektrik a na obrázku):

  \[|\Delta\varphi| = \left|\int_{\mathrm{sipky}} \vec E\,\cdot\,d\vec r \right|=.\]

  Protože pole je v každém bloku homogenní, dostáváme

  \[ =\int_0^\mathrm{a} E_1\,dr + \int_a^\mathrm{2a} E_2\,dr = E_1\int_0^\mathrm{a} dr + E_2\int_\mathrm{a}^\mathrm{2a} dr = E_1a+E_2a = \frac{7\sigma a}{6\varepsilon_0}.\]

• Řešení částí (e) a (f)

  (e) Objemový vázaný náboj ρ_b je nulový, neboť polarizace obou bloků je homogenní, a tudíž

  \[\varrho_\mathrm{b} = -\nabla\,\cdot\,\vec P = 0.\]

  Divergence vektoru polarizace je nulová. Plošný vázaný náboj má hustotu

  \[\sigma_\mathrm{b,1} = \vec P_1 \,\cdot\,\vec n = \pm P_1 = \pm \frac{\sigma}{2}\]

  na krajích prvního bloku, neboť jednotkový vektor \(\vec n\) vnější normály k povrchu a vektor polarizace mají stejný směr a opačnou či stejnou orientaci; přičemž na kraji v blízkosti elektrody má tento náboj zřejmě opačné znaménko, než je náboj elektrody. Obdobně má plošný vázaný náboj hustotu

  \[\sigma_\mathrm{b,2} = \vec P_2 \,\cdot\,\vec n = \pm P_2 = \pm \frac{\sigma}{3}\]

  na krajích druhého bloku (přičemž na kraji v blízkosti elektrody má tento náboj opět opačné znaménko, než je náboj elektrody).

  (f) Intenzita pole v okolí velké roviny má velikost

  \[E = \frac{\sigma}{2\varepsilon_0}\]

  v celém prostoru, vektor intenzity má směr kolmý k rovině, orientace závisí na znaménku náboje desky (při kladném míří od roviny, při záporném k ní).

  Připomeňme, že tento fakt vyplyne například použitím Gaussovy věty na stejný kvádr jako v části (a), jen si je třeba uvědomit, že při přítomnosti jediné roviny pole teče oběma podstavami kvádru rovnoběžnými s rovinou (odtud jedna polovina ve výrazu napravo).

  

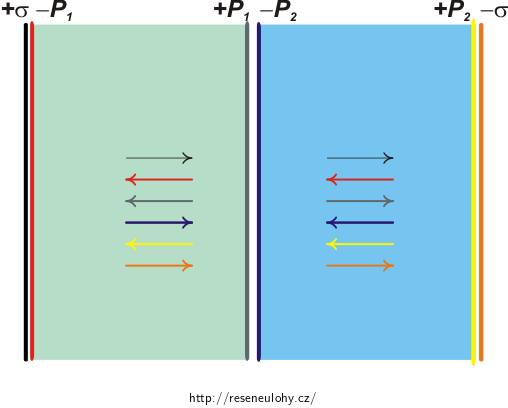
  Tento vztah použijeme na celkem šest rovin, které nesou rovnoměrně rozložený náboj: dvě elektrody nesoucí volný náboj o hustotě \(\pm\sigma\) a čtyři roviny nesoucí vázaný povrchový náboj o hustotách \(\pm \sigma/2\), \(\pm \sigma/3\). Uvědomte si také, že namísto dielektrik nyní při výpočtu uvažujeme mezi deskami vakuum a roviny s vázanými náboji: ε₀ je tedy na místě ve všech vztazích!

  Pro prostor prvního dielektrika dostáváme (uvědomte si orientace intenzit polí jednotlivých desek s volným či vázaným nábojem, jak naznačují šipky na obrázku výše):

  \[E_1 = \frac{\sigma}{2\varepsilon_0} - \frac{\sigma/2}{2\varepsilon_0} - \frac{\sigma/2}{2\varepsilon_0} + \frac{\sigma/3}{2\varepsilon_0} - \frac{\sigma/3}{2\varepsilon_0} + \frac{\sigma}{2\varepsilon_0} = \frac{\sigma}{2\varepsilon_0}.\]

  Pro prostor druhého dielektrika dostáváme:

  \[E_2 = \frac{\sigma}{2\varepsilon_0} - \frac{\sigma/2}{2\varepsilon_0} + \frac{\sigma/2}{2\varepsilon_0} - \frac{\sigma/3}{2\varepsilon_0} - \frac{\sigma/3}{2\varepsilon_0} + \frac{\sigma}{2\varepsilon_0} = \frac{2\sigma}{3\varepsilon_0}.\]

  To je v souladu s výpočtem v části (b).

• Odpověď

  (a) Elektrická indukce má velikost D = σ mezi elektrodami, směr kolmý na elektrody a orientaci od kladné elektrody k záporné. Vně kondenzátoru je elektrická indukce nulová.

  (b) Elektrická intezita má stejný směr a orientaci jako elektrická indukce. V bloku o relativní permitivitě 2 má velikost E₁ = σ/2ε₀, v bloku o relativní permitivitě 1,5 má velikost E₂ = 2σ/3εq₀.

  (c) Vektor polarizace má stejný směr a orientaci jako elektrická indukce. V bloku o relativní permitivitě 2 má velikost P₁ = σ/2, v bloku o relativní permitivitě 1,5 má velikost P₂ = σ/3.

  (d) Potenciálový rozdíl mezi elektrodami je

  \[|\Delta\varphi| = \frac{7\sigma a}{6\varepsilon_0}.\]

  (e) Hustota objemového vázaného náboje je nulová. Na površích dielektrika s relativní permitivitou 2 je hustota povrchového vázaného náboje ± σ/2, na površích dielektrika s relativní permitivitou 1,5 je hustota povrchového vázaného náboje ±σ/3. Přitom kladný, resp. záporný vázaný náboj se rozmístí v blízkosti záporné, resp. kladné elektrody.

  (f) Výpočet dává stejný výsledek jako v části (b).